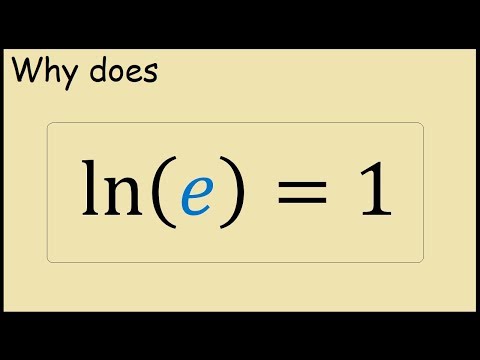Ln 1 E

I ve looked through my book and it lists the natural logarithms properties but i can t find why ln 1 e 1.

Ln 1 e. The limit of natural logarithm of infinity when x approaches infinity is equal to infinity. Ln 1 ln e 0 1 1 thus we have our answer. So let us compute them all. Ln 1 e ln 1 ln e 1 anything to the power 0 1 2 ln e 1 as the base of natural logarithms is always e here we can simplify.

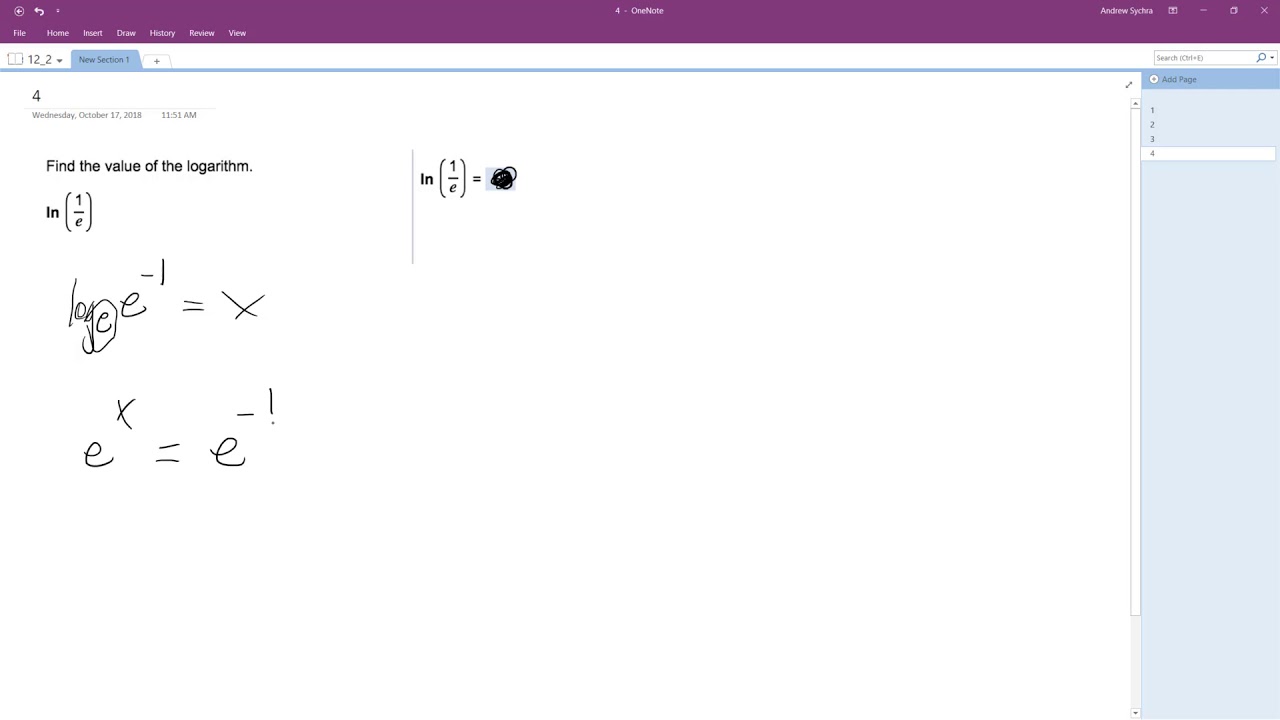
1 division rule of logarithms states that. Ln e log e e ln e is the number we should raise e to get e. Ln 1 e ln e 1 1 since for any value x ln e x x 0 0 0. Ok we have to compute three taylor coefficients.

E 1 e. Ln 1 e is a complex value 1 πi response. No flaw comes from the fact that that complex natural log is a multivalued function and in fact you can add any multiple of 2πi to the solution and still have it be correct. You can sign in to give your opinion on the answer.

The natural logarithm of zero is undefined. The natural logarithm can be defined for any positive real number a as the area under the curve y 1 x from 1 to a the area being taken as negative when a 1. The natural logarithm of a number x is defined as the base e logarithm of x. Ln x log e x so the natural logarithm of e is the base e logarithm of e.

Ln 1 e 1 why. So the natural logarithm of e is equal to one. Log in to reply to the answers post. Yes it is 1 because ln is base e and you can rewrite 1 e as e 1.

Ln e x 1 ln e x color blue ln e x 1 x i don t know if this is a simplification per se but it s definitely a valid way to rewrite the function. The natural logarithm of one is zero. Ln e log e e 1. Natural logarithm of infinity.

The limit near 0 of the natural logarithm of x when x approaches zero is minus infinity. Ln x y ln x ln y here we can substitute. What do you think of the answers.